IFS Fractals
IFS (Iterated Function System) fractals are generated using a linear algebra concept called affine transformations. They're known to be remarkably adept at modeling shapes found in nature (plants being an excellent example). The tree fractal IFS values were taken from this website which has a good selection of various types of fractals.
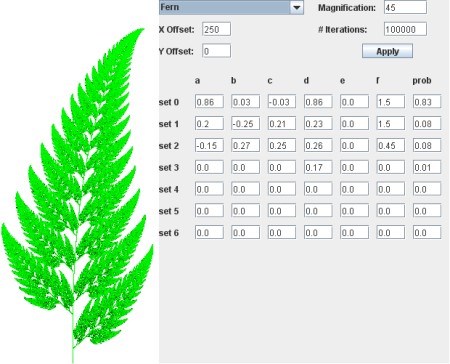
Features:
- Select from several preprogrammed fractals
- Select custom IFS matrix values by selecting "Custom" from the drop-down menu
How it Works:
Affine Transformations:
An affine transformation has the following form where a-f are constants:
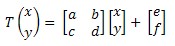This can also be written without matrices like so:
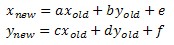
Iterated Function System (IFS) Fractals:
An IFS is an (n x 7) matrix in which each row contains the a-f values of an affine transformation plus a column representing the probability of that transformation being chosen.
Below is an IFS describing a Barnsley Fern.
Based on this IFS we can see that the most likely transformation to take place is:
The algorithm involved in drawing an IFS fractal is as follows:
- Start at a random point.
- Pick a random transformation from the IFS (remembering to account for the weighted probabilities).
- Apply the transformation to our current point to get our new point.
- Draw a dot at our new point.
- Go back to step 2 and repeat this process several thousand times.