The Mandelbrot is one of the most famous fractals for good reason. It's a wonderful example of infinite resolution and the beauty that can be created from a relatively simple function.
Instructions:
- Left-click and drag to move.
- Right-click and drag down or up to zoom in or out respectively.
- Hold down both left and right mouse buttons and drag to form a new a viewing area. Left-click to confirm the selection, or right-click to cancel.
- Move the bar at the bottom to set the number of calculations done. Higher settings are required to view small details when zoomed in, while lower settings work well when zoomed out.
- The coordinates are shown in the textboxes to the right, and can be saved by copying the coordinates into a text editor and later copying them back into the program. Be sure to click APPLY to move the new coordinates you enter.
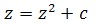Another form that is perhaps more descriptive:
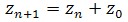
The Mandelbrot Set contains all points that remain bounded (don't go to infinity) with repeated application of the function. Our test to see if a point is bounded is that if a point goes beyond a radius of 2 from the origin then we know it will go to infinity. However, we can't tell for certain whether a point is bounded since it may take it 2000 iterations to go past the radius of 2 when we're only calculating 1999 iterations.
Since the Mandelbrot set is indeed a set, with points either being in the set or out, one might wonder why it's colored in not just black and white, but shades of gray and even colors. This is because depictions of the Mandelbrot almost always show not just whether points are inside the set or not, but also how fast the points that aren't in the set manage to escape the barrier of radius 2. For instance, my program defaults to points within the set being colored white and those that escape in one iteration being black. So if we're running our function a maximum of 100 iterations and input a point that escapes within 15 iterations it will be drawn as a dark gray.